学习这个知识点我们主要有3个目标:

这一节知识点的重点难点分别是:
重点:让学生理解绝对值的概念,并掌握求一个已知数的绝对值的方法。
难点:绝对值的几何意义和代数定义的导出与对“负数的绝对值是它的相反数”的理解。
绝对值如何理解?
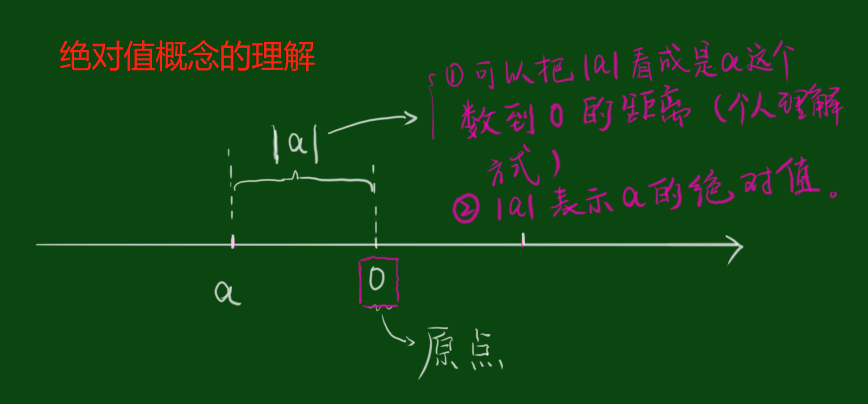
我们对绝对值的定义是:一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a |。 (这里的数a可以是正数、负数和0)。
我们通过看它的概念可以了解到,它是真的需要借助数轴的来形象的理解。比如一个数a,我们现在在数轴上找到这个数的位置。然后看它到原点的距离有多远?这个距离的长度就是a的绝对值。我们用|a |表示它。
接下来我们就是研究求绝对值的过程中,找一些普遍的规律。比如我们发现3的绝对值是3,-3的绝对值也是3。我们发现两个数如果互为相反数,他们的绝对值会相等。而任何数的绝对值都不可能是一个负数,而是一个非负数。也就是一个大于等于0的数。
求一个数的绝对值的方法:
去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的意义去掉绝对值符号,总之要确保其结果为非负数且只有一个。随着研究的深入我们又发现,直接求一个数的绝对值是一个解;若已知一个数的绝对值,反过来求这个数,则有两个解.即如果|x|=a(a>0),则x=±a。
比如|-5|是等于5,而一个数的绝对值等于5,这样的数有两个,分别是-5,5。因为在数轴到原点的距离等于5的数是有两个的。
接着我们又对绝对值的知识点进行了一个拓展,我们两个负数比较大小的时候,以前我们是在数轴上来直观比较。因为我们发现数轴的数是这样的一个规律,右边的总是比左边的大。而当我们学会了绝对值的时候,我们发现负数之间比较大小的时候。小的那个数它的绝对值反而比较大!所以我们就可以得到这样一个结论。
两个负数比较大小,绝对值大的那个数反而小!比-5与-8比较大小的时候,我们在数轴上表示的时候,-5是在-8的右边的。所以-5>-8。而当我们去研究这两个数的绝对值的时候,发现-8的绝对值是大于-5的绝对值的。